
Continuity over other types of intervals are defined in a similar fashion. Analogously, a function f ( x ) f ( x ) is continuous over an interval of the form ( a, b ] ( a, b ] if it is continuous over ( a, b ) ( a, b ) and is continuous from the left at b. A function f ( x ) f ( x ) is continuous over a closed interval of the form if it is continuous at every point in ( a, b ) ( a, b ) and is continuous from the right at a and is continuous from the left at b. Ī function is continuous over an open interval if it is continuous at every point in the interval. Ī function f ( x ) f ( x ) is said to be continuous from the left at a if lim x → a − f ( x ) = f ( a ).

These examples illustrate situations in which each of the conditions for continuity in the definition succeed or fail.Ī function f ( x ) f ( x ) is said to be continuous from the right at a if lim x → a + f ( x ) = f ( a ).
Continuity calculus problems how to#
The next three examples demonstrate how to apply this definition to determine whether a function is continuous at a given point. If lim x → a f ( x ) = f ( a ), lim x → a f ( x ) = f ( a ), then the function is continuous at a. If lim x → a f ( x ) ≠ f ( a ), lim x → a f ( x ) ≠ f ( a ), then the function is not continuous at a.

Problem-Solving Strategy: Determining Continuity at a Point At the very least, for f ( x ) f ( x ) to be continuous at a, we need the following condition: We see that the graph of f ( x ) f ( x ) has a hole at a. Our first function of interest is shown in Figure 2.32. We then create a list of conditions that prevent such failures. Continuity at a Pointīefore we look at a formal definition of what it means for a function to be continuous at a point, let’s consider various functions that fail to meet our intuitive notion of what it means to be continuous at a point. Intuitively, a function is continuous at a particular point if there is no break in its graph at that point. We begin our investigation of continuity by exploring what it means for a function to have continuity at a point. They are continuous on these intervals and are said to have a discontinuity at a point where a break occurs. Other functions have points at which a break in the graph occurs, but satisfy this property over intervals contained in their domains. Many functions have the property that their graphs can be traced with a pencil without lifting the pencil from the page.
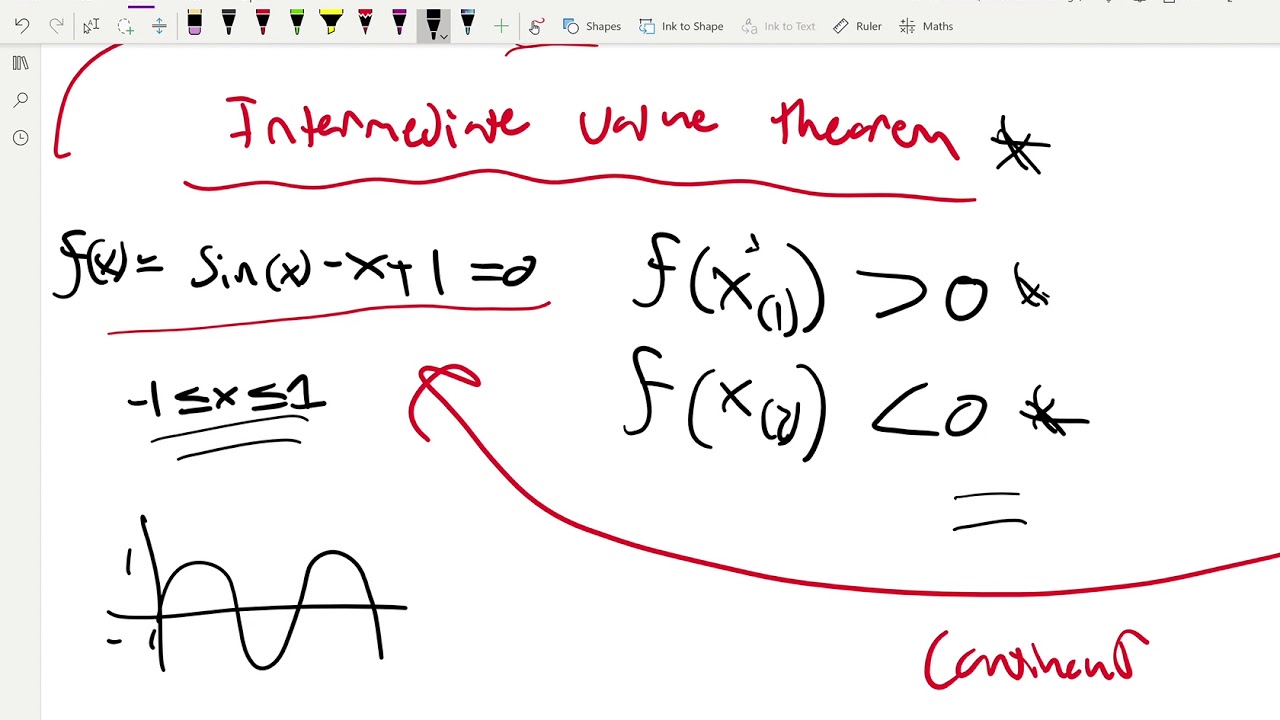
2.4.3 Define continuity on an interval.2.4.2 Describe three kinds of discontinuities.2.4.1 Explain the three conditions for continuity at a point.


 0 kommentar(er)
0 kommentar(er)
